Kopelkiden-Definition

Definition:
In einem n-dimensionalen metrischen Raum (M, d) bewegen sich zeitgleich n Punkte Pn(t). Die Bahn eines Punktes A(t) innerhalb dieses Raumes heißt Kopelkide, wenn die Abstände dn dieses Punktes zu jeder Zeit t zu allen Punkten Pn(t) jeweils konstant sind.
Der Punkt A heißt Kopfpunkt, die Punkte Pn sind die Leitpunkte, sie bewegen sich auf den Leitlinien.
Die Kopelkide heißt starr, wenn auch die Abstände aij der Leitpunkte zueinander zeitlich konstant sind.
Anwendungsbeispiel aus der Technik
Fußpedal Modibike
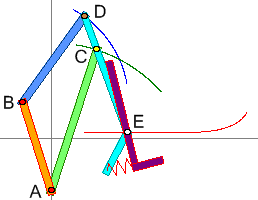
Im obigen Bild sieht man einen Verladekran umfunktioniert als Fahrradpedale. Der gelbe Leitpunkt C bewegt sich auf dem grünen Kreisbogen um A, der braune Leitpunkt D auf dem blauen Kreisbogen um B. Der weiße Kopfpunkt E hat zu jeder Zeit den gleichen Abstand zu C und D, er bewegt sich auf der roten Kopelkiden. Da der Abstand der beiden Leitpunkte C und D stets gleich ist, handelt es sich um eine starre, 2-dimensische Kopelkide der Ebenen. ("2-dimensisch" bezieht sich auf den Raum und nicht auf die Kopelkide, denn die sind immer eindimensional.)
Satz der Kopelkiden-Bedingung:
Ist der metrische Raum M vollständig und stetig infinit normiert und gilt Pi(t) ≠ Pj(t) für alle t ∈ ℝ , dann ist mindestens eine Kopelkide eindeutig bestimmt, wenn gilt:
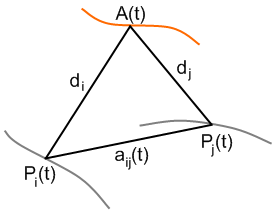
Dabei meint di den stets konstanten Abstand des Kopfpunkts A(t) vom Leitpunkt Pi(t), (i ≤ n) und aij(t) den Abstand des Leitpunkts Pi(t) vom Leitpunkt Pj(t).
Stetig infinit normiert heißt, es gibt keine Obergrenze für den Abstand und es gibt keine Lücken im Wertebereich bei der Abstandsdefinition. Der Wertebereich der Abstandsnorm ist W = { [0, ∞] }.
Beweis:
Da es sich um einen metrischen Raum handelt, gilt die Dreiecksungleichung. Hier also:
a ij(t) ≤ d i + d j
d i ≤ a ij(t) + d j
d j ≤ a ij(t) + d i
Gibt es für den Abstand eine Obergrenze (wie z.B. die Zahl π als Abstand von Pol zu Pol bei der Einheitskugel mit euklidischer Abstandsnorm), dann dürfen die Abstände des Kopfpunktes von den Leitpunkten diese Grenze nicht überschreiten, denn sonst kann man sie nicht messen.
Anzahl der Kopelkiden
Zur Anzahl der möglichen Kopelkiden kann man so ohne weiteres nichts sagen. Die hängt ab vom Raum. Klar ist, dass es auf einer Kugeloberfläche bzw. Ebenen (die Ebene kann man als eine Kugel auffassen mit Radius unendlich) entweder 0, 1, 2 oder unendlich viele gibt. Der Beweis erfolgt algebraisch: man stellt die Formel für alle Schnittpunkte zweier Kreise auf einer Kugeloberfläche auf. Das führt dann zu einer Wurzelgleichung mit zwei Lösungen, wenn die beiden Kreismittelpunkte nicht auf ein und derselben Ursprungsgeraden liegen.
Auf einem Zylindermantel kann es z.B. 4 Berührungspunkte geben und damit ist die Anzahl dort: {0, 1, 2, 3, 4, ∞}.
Auf einem Seestern mit 5 Strahlen kann es abzählbar bis zu 10 geben.
3D-Stereoskopie Zylindermantel
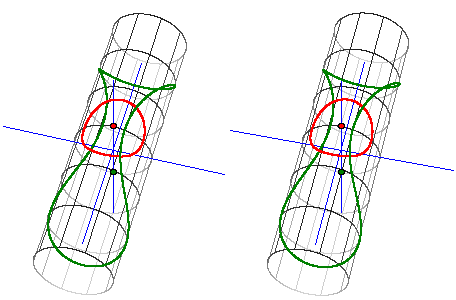
Punkte der grünen/roten Kurve haben den gleichen Abstand vom grünen/roten Punkt
4 Schnittpunkte
(mit dem linken/rechten Auge auf das rechte/linke Bild schauen
und dann beide Bilder zur Überdeckung bringen)
4 Schnittpunkte
(mit dem linken/rechten Auge auf das rechte/linke Bild schauen
und dann beide Bilder zur Überdeckung bringen)
Beispiel: Unstetigkeit
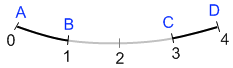
Kurvenstück mit Metrik und Sprung
Das Bild zeigt einen 1-dimensionalen Raum mit Metrik. Punkte sind nur dort zugelassen, wo die Kurve schwarz ist. Zwischen den Punkten B und C klafft eine Lücke der Länge 2. Der Wertebereich der Abstandsnorm ist also:
W = {[0, 1] und [2, 4]} .
Für die Abstandswerte ]1, 2[ und ]4, ∞[ gibt es im obigen Beispiel keine Punkte-Paare. Die drei Axiome des metrischen Raumes sind erfüllt trotz "Sprung". Die Abstandsnorm ist nicht stetig und nicht unendlich.
Satz:
Sind die Bewegungen der Leitpunkte periodisch und stehen die Periodendauern in einem rationalen Verhältnis zueinander, dann sind die Kopelkiden geschlossen, wenn die Kopelkiden-Bedingung stets erfüllt ist.
Beweis:
Nimmt man O.B.d.A zwei Periodendauern heraus, dividiert man die kleinere Periodendauer Ti durch die größere Tj, dann ergibt sich eine rationale Zahl, die man als a / b schreiben kann mit a, b ∈ ℕ.
Durchläuft man nun b mal die Periodendauer, dann hat Pj auch b mal seine Periode durchlaufen und entsprechend Pi b mal a / b, also a mal. a und b sind natürliche Zahlen, also stehen beide Punkte gleichzeitig wieder am gleichen Ort. Nun kann man beide Periodendauern zu einer neuen Periodendauer a*Ti = b*Tj zusammenfassen und das gleiche Verfahren auf eine nächste Periodendauer Tk des Leitpunktes Pk anwenden und so fort, bis alle Leitpunkte abgearbeitet sind.
Da die di, dj ... nicht zeitabhängig sind, befinden sich damit auch alle Kopfpunkte wieder am gleichen Ort. q.e.d.
Eine 2-dimensische (ebene) Kopelkide
(Double Dog)
(Double Dog)
Herrchen und Frauchen pendeln um eine Kreisbahn -
Der Hund in der Mitte hält immer den Abstand zu beiden
Der Hund in der Mitte hält immer den Abstand zu beiden
Die Bezeichnung "Double Dog" leitet sich von den Hundekurven (Traktrix) ab, die nur ein Herrchen im 2-dimensionalen haben.
eine andere Kopelkide
Lässt man die Bahnen von Herrchen und Frauchen variieren, dann variiert auch die Kopelkide. Es ergeben sich schöne Animationen wie hier:

Seerose
Und das Schönste: der Formenreichtum ist unendlich und viele von ihnen lassen sich leicht in Holz basteln!
